Relativitätstheorie und Zeit

Das Problem fängt damit an, dass Licht etwas sehr eigenartiges ist: Licht hat immer - ganz egal in welchem Bezugsystem man misst - dieselbe Geschwindigkeit, nämlich ca. 300000km/s. Was ist daran so eigenartig?

Nehmen wir mal an, dass in einem fahrenden Zug ein Ball geworfen wird. Wenn der Ball im Zug mit 5m/s nach vorne fliegt und der Zug selbst mit der Geschwindigkeit 25m/s fährt, dann sieht die Person im Zug den Ball mit einer Geschwindigkeit von 5m/s fliegen. Für die Person außerhalb des Zugs fliegt der Ball mit 30m/s vorbei, da der Zug ja schon 25m/s hat. So ist z.B. eine Fliege, die im Flugzeug nach vorne fliegt, schneller als das Flugzeug. Für Geschwindigkeitsangaben ist eigentlich immer die Angabe des Bezugsystems nötig. (Wenn klar ist, dass man sich z.B auf die Erde bezieht, läßt man die Angabe des Bezugsystems weg.) Nochmal der Ball im Zug: Bezüglich des Zugs ist der Ball 5m/s schnell. Bezüglich des Bahndamms ist der Ball 30m/s schnell. Würde der Ball nicht nach vorne sondern nach hinten mit 5m/s geworfen, dann wäre er: Bezüglich des Zugs immer noch 5m/s schnell (nur jetzt halt nach hinten). Bezügich des Bahndamms jedoch nur noch 20m/s schnell, da er sich entgegengesetzt zum Zug bewegt. Und nun zum Licht: Schaltet man eine Taschenlampe an, dann bewegt sich das Licht analog zum Ball (nur sehr viel schneller). In Fahrtrichtung des Zugs müsste man von außen eine etwas höhere Lichtgeschwindigkeit messen als im Zug, nämlich gerade um die Geschwindigkeit des Zugs mehr. Das Ergebnis ist jedoch: Ganz egal ob man im Zug oder außerhalb misst, ob die Lampe nach vorne oder nach hinten strahlt, man erhält immer die gleiche Zahl, nämlich 300000km/s (Exakt: 299792,458km/s). Weiter gilt: Kein Körper kann auf eine größere Geschwindigkeit als Lichtgeschwindigkeit beschleunigt werden. Genaugenommen kann kein Körper je auf Lichtgeschwindigkeit beschleunigt werden. (Die Lichtteilchen werden nicht auf Lichtgeschwindigkeit beschleunigt: sie haben Lichtgeschwindigkeit.)

Diese Konstanz der Lichtgeschwindigkeit hat aber nun zur Folge, dass eine Uhr in einem fahrenden Zug anders gehen muss als in einem stehenden. Für den Beobachter im Zug und den Beobachter außerhab des Zugs vergeht die Zeit verschieden schnell. (Dieser Effekt hängt natürlich von der Geschwindigkeit des Zugs ab und wird erst beobachtbar, wenn der Zug eine Geschwindigkeit hat, die in der Größenordnung der Lichtgeschwindigkeit liegt - was bei Zügen wohl nicht geht. Die schnellsten Menschen waren die Astronauten, die zum Mond geflogen sind, sie waren 10km/s schnell. Das ist schnell, aber im Vergleich zur Lichtgeschwindigkeit mit 300000km/s langsam.)

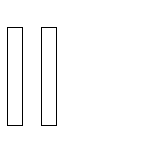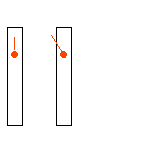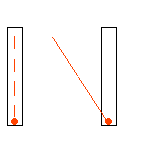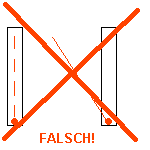
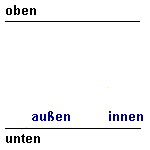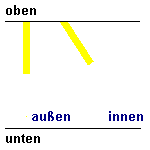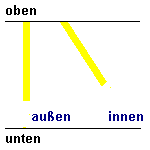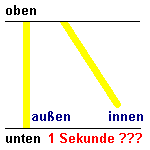
Wir stellen uns einen Zug vor, der sehr schnell ist, z.B. halbe Lichtgeschwindigkeit hat. (Vorstellen kann man sich ja viel.) In diesem Zug schalten wir an der Decke ein Licht ein und messen, wann der Lichtstrahl am Boden ankommt. Diese Zeit soll die Basis unserer Uhr sein. Als Gedankenexperiment kann man sich ja alles mögliche vorstellen. Wenn wir uns vorstellen, dass der Zug 300000km hoch ist, dann müsste das Licht nach einer Sekunde am Boden eintreffen. (Wenn ihr euch den Zug nicht ganz so hoch vorstellen wollt, dann ist die Zeit eben kürzer, kann aber ebenfalls als Basis einer Uhr genommen werden.) Der Beobachter im Zug schaltet also seine Lampe ein, und wenn der Lichtstrahl unten angekommen ist, ist für ihn eine Sekunde vorbei. Der Beobachter außerhalb des Zugs hat auch eine solche Uhr. Er schaltet ebenfalls die Lampe an der Decke an und wenn bei ihm das Licht unten angekommen ist, ist für ihn eine Sekunde vorbei. Zusätzlich schaut dieser Beobachter auch in den Zug und sieht dort die "Uhr" laufen. Und jetzt wird es eigenartig: Für den Beobachter außerhalb des Zugs ist der Weg von der Deckenlampe im Zug bis zum Boden jedoch länger, da der Zug sich ja weiterbewegt. Die obere Animation trifft für Bälle zu (die langsamer als Lichtgeschwindigkeit sein müssen! s.o.) aber nicht für das Licht. In der oberen Animation ist bei der fahrenden "Uhr" die Strecke deutlich länger. Wenn beidesmal die Bälle in einer Sekunde unten ankommen sollen, muss rechts der Ball schneller sein. (Ist er auch, er hat ja zusätzlich noch die Geschwindigkeit des Zugs.) Bei Licht geht dies aber nicht! Die Lichtgeschwindigkeit ist ja unabhängig vom Bezugsystem immer gleich. Somit verhält sich das Licht so wie in der unteren Animation gezeigt: Die Strecke, die das Licht in der ruhenden "Uhr" zurücklegt und die Strecke, die das Licht in der fahrenden "Uhr" zurücklegt, ist jeweils gleich. Und dann reicht es eben rechts in der fahrenden "Uhr" nicht ganz nach unten. Die Zeit in dem fahrenden Raum verläuft langsamer!

Der Beobachter in dem bewegten Raum bemerkt nichts von seiner "langsameren" Uhr, für ihn vergeht die Zeit ganz normal, wie auch für den ruhenden Beobachter. Der Unterschied wird erst bemerkbar, wenn diese beiden sich treffen: Dann ist der bewegte weniger gealtert als der ruhende. Dieser doch recht eigenartige Sachverhalt ist durch Experimente überprüft und bestätigt worden. Die Zeit ist keine absolut ablaufende Größe, die Zeit hängt von der Bewegung des Raums ab. (Je mehr sich die Geschwindigkeit der Lichtgeschwindigkeit nähert, umso langsamer verläuft die Zeit.) Da die Zeit vom Raum abhängt, wird in der aktuellen Physik auch von "Raumzeit" gesprochen, was bedeutet, dass Raum und Zeit zusammenhängen.